Have you ever wondered how Google Maps can calculate driving directions so fast? Google can calculate driving directions in 100-500 milliseconds, whereas back in 1990s it took my father's 386sx about 30 minutes to calculate such a route.
If you've done much programming, you probably already know the basics of this. Road maps can be represented, in the jargon, as "graphs", where junctions are "nodes" and roads between junctions are "edges" and the time taken to drive down each edge is its "cost". Finding the fastest route between two locations is then a matter of finding the shortest path between nodes of the graph.
Traditional algorithms for finding such routes include Dijkstra's Algorithm and the A* algorithm. If you haven't heard of those, go read the wikipedia pages - because the rest of this post is going to assume you know them!
There are several algorithms that are a lot faster and more memory efficient than Dijkstra's Algorithm. They rely on doing a bunch of time-consuming preprocessing on the graph; once the graph is processed individual queries can run a lot faster. This post is about the "contraction hierarchies" algorithm, one of the simpler algorithms that does this.
This algorithm isn't my invention - it was proposed by Robert Geisberger, Peter Sanders, Dominik Schultes, and Daniel Delling of Universitat Karlsruhe - and I can't guarantee Google use this specific algorithm. I'm sure they use something similar, though!
Preprocessing the graph
We preprocess the graph by "contracting" the nodes one at a time.Wondering how we choose the order? Read on to find out We number nodes in the order we contract them. To perform the contraction we work out every shortest path between the node's immediate neighbors and insert "shortcuts" for them, then we mark the node as processed.
Here's a simple graph, before and after a node is contracted:
To contract C we insert shortcuts from A to E and from A to B because A->C->E and A->C->B are shortest routes. We don't need to insert a shortcut from B to E because B->C->E isn't the shortest route from B to E. B->D->E is shorter.
Contracting doesn't completely delete a node - but the node can be ignored for the rest of the contraction process, because when we see an edge going toward C we know there's either a shortcut or it isn't a shortest path; either way, we don't need to visit C. If we do a search that starts or ends at C we'll still be able to find it - you'll see how later in the post.
What about when there are two routes to an end point, both routes exactly the same length? If you want to find all such routes, you should insert a shortcut whenever it's the same length as the shortest path; if you don't want multiple results, you only need to insert shortcuts when they're the only shortest path. Two routes exactly the same length is unusual with the way roads are usually laid out in the UK, but it might be relevant in cities laid out as grids, or when pathfinding for video game AIs where the game uses a grid layout.
A visualisation of the contraction process
Here's an animation showing the contraction process.
- Cyan markers identify individual nodes
- Node heights indicate their position in the contraction order - the highest being nodes that haven't been contracted yet
- Blue lines are edges from the original graph.
- Green lines mark where shortcuts are inserted.
- White lines show the original graph in 2D, for comparison.
As this is implemented in three.js you should be able to scroll around with gestures, or with your mouse or keyboard - give it a go!
So how come the nodes get contracted in that order?
The algorithm will produce correct results regardless of the contraction order - but how much of a performance improvement you get depends on the contraction order.
Papers on the algorithm have evaluated several heuristics to choose node orders.
Usually we prefer contractions that reduce the number of edges, after added shortcuts are taken into account. Better to do a contraction that removes five edges than a contraction that only removes four!
We also try to keep contraction depths roughly even across the map - if you had a hundred nodes in a row and you contracted them from right to left, you wouldn't have to add any shortcuts - but to path from one end to the other you'd have to visit every node. On the other hand if you contract every other node the contracted graph will look more like a binary tree, and the search process will have to visit fewer nodes.
There are a bunch of other heuristics you can apply - see the paper linked above for examples.
Finding the shortest path
To find the shortest path between two nodes we perform two searches - one from the start node, one from the end node - then we see where they meet. Let's assume we want to find the route between node 1 and node 8.
Search from the start node
The search is similar to Djikstra's algorithm - but with one extra rule: We only follow edges going to nodes with a higher contraction order than the current node. In our visualisation, this means we only ever follow edges that slope upwards:
Search from the end node
The search from the end node works the same way. If your graph has directed edges, the search from the end node will go follow edges in the reverse direction. For simplicity, all edges in this visualisation are bidirectional.
Combining the forward and reverse searches
We take the lists of nodes visited in the forward and reverse searches and find the intersection.
From node 1:
Node 1 reached immediately Node 2 reached at cost 1, via 1->2 Node 9 reached at cost 4, via 1->2->9 (2->9 via shortcut 2->7->9)
From node 8:
Node 8 reached immediately Node 3 reached at cost 1, via 8->3 Node 7 reached at cost 1, via 8->3 Node 9 reached at cost 1, via 8->9 Node 2 reached at cost 2, via 8->3->2 Node 4 reached at cost 2, via 8->3->4
Putting one route after the other, we cna get from node 1 to node 8 via 1->2->3->8 at cost 3.
If the result sets had several entries in common, we would choose the one with the lowest cost.
Visiting eight nodes out of ten doesn't seem like much of an improvement?
Right, but drawing ten nodes makes for a simpler animation! Let's look at a 40x2 grid, with a total of 80 nodes:
The first search sequence visits 11 nodes, the second search 13. That's a total of 24 nodes out of 80 visited, to discover a path 39 segments long.
So what would a search of an entire country involve?
I live in the UK, so I've been processing OpenStreetMap data for the UK.
Below you can see the two searches required to find the shortest path between Albert Drive in Glasgow and Herbal Hill in Islington, London. The map is shown as a png because the interactive map usually gives me an 'unresponsive script' warning.
The search starting in Edinburgh is shown in blue; the search starting in London in red; and the shortest path in black.
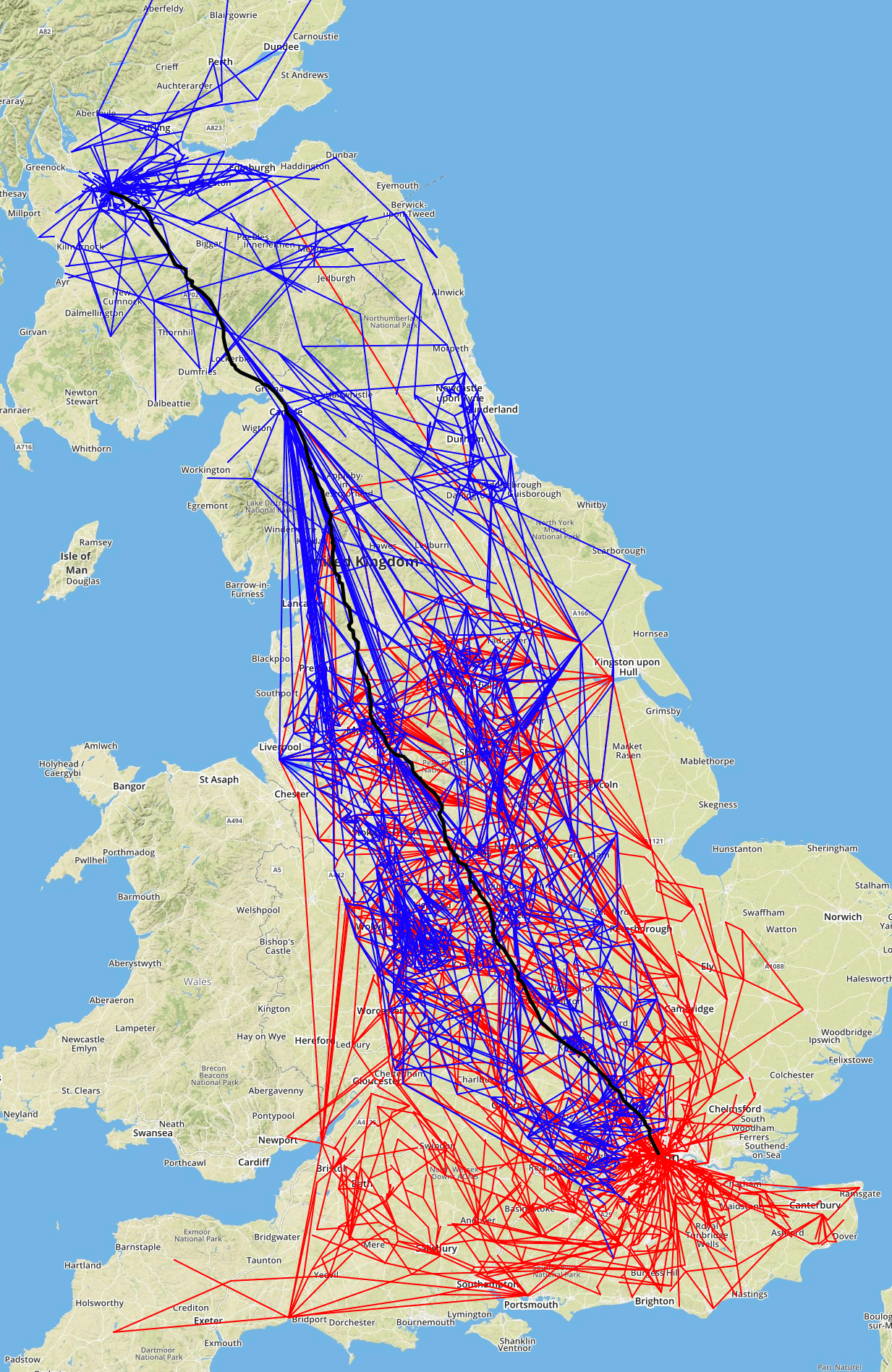 Tiles © Mapbox, Map data © OpenStreetMap.
Tiles © Mapbox, Map data © OpenStreetMap.
The UK map data contains 3,478,051 nodes and 7,646,738 (non-shortcut) edges. The contraction process added 6,186,168 shortcuts.
The searches from London and Edinburgh visited at 3,968 and 3,113 nodes respectively, and the solution path found passed through 3,617 nodes.
For my implementation, the search process took 18ms - plenty fast enough for the 500ms response times Google provides! Contraction for the UK took 55 minutes using a single core on a modern i7 processor, and needed about 10 GB of RAM. You could make the process more RAM- and CPU-efficient if you wanted to!
More info and similar algorithms
- Hannah Bast from Universität Freiburg has a nice set of lectures on route planning - I figured out most of my implementation from lecture slides like these, because papers containing symbols like ∀ and ⊆ intimidate me :)
- Robert Geisberger's 2008 thesis provides lots more details on contraction hierarchies, and comparisons to other algorithms.
- Highway Hierarchies divides the road network into neighborhoods and highways. Personally I found Sanders and Schultes's algorithm harder to understand than contraction hierarchies, but they report good performance.
- Transit node routing identifies important traffic junctions (such as freeway and motorway onramps) and creates a lookup table containing the shortest paths between all such junctions.
- Travel networks with timetables or varying road speeds have also been addressed by Geisberger as have one-to-many travel time computations.
- A google tech talk by Peter Sanders covers quite a bit about fast route planning.
Conclusion
The contraction hierarchies algorithm is actually fairly simple, and makes path finding very quick - easily below the 100ms industry standard for web pages. If you only want to know total travel time, you have to visit fewer nodes than there are in the path!
The animated 3D graphics were made using three.js - previously my only 3D experience has been with JOGL and I have to say I found three.js a lot easier!
At the time of writing, there's an OpenStreetMap fundraising drive to upgrade a database server? I couldn't have written this post without their map data, and the project has an annual budget of just $85k. Maybe you'd like to donate?
